Kuiper Deep Learning Inference Framework
Introduction
什么是推理框架?
深度学习推理框架用于对已经训练完成的神经网络模型文件进行加载,并根据模型文件中的网络结构和权重参数对输入图像进行预测。换句话说,深度学习推理框架就是将深度学习训练框架Pytorch和TensorFlow中训练完成的模型,移植到中心侧和端侧并且在运行时高效执行。另外,与深度学习训练框架不同的是,推理框架没有梯度后向传播的过程,因为在推理阶段模型的权重已经固定,不需要利用后向传播技术进一步进行调整。
例如对于一个Resnet分类网络的模型,深度学习推理框架先对模型文件中的网络结构进行读取和载入,再读取模型文件中的权重参数和其他参数、属性信息填入到Resnet网络结构中,随后推理框架将不同的图像放入到计算图的输入中,并执行预测过程,从而得到其归属的类别。以下的图示是我对如上内容的总结:

KuiperInfer Overview
KuiperInfer可以分为以下的几个��模块:
Operator:深度学习计算图中的计算节点,包含以下的几个部分:- 存储输入输出的张量,用于存放深度学习中各层的输入输出。比如对于一个
Convolution层,需要一部分空间来保存计算的输入和输出。 - 计算节点的类型和名称,计算节点类型可以有
Convolution,Relu,Maxpooling等,计算节点的名称是唯一的,用来区分任意一个节点,可以是Convolution_1,Convolution_2等。 - 计算节点的参数信息,例如卷积中的步长、卷积核的大小等。
- 计算节点的权重信息,例如卷积节点中的
weight,bias权重。
- 存储输入输出的张量,用于存放深度学习中各层的输入输出。比如对于一个
Graph:- 有多个
Operator串联得到的有向无环图,规定了各个计算节点(Operator)执行的流程和顺序。
- 有多个
Layer:- 计算节点中运算的具体执行者,
Layer类先读取输入张量中的数据。 - 然后对输入张量进行计算,得到的结果存放到计算节点的输出张量中,当然,不同的算子中
Layer的计算过程会不一致。
- 计算节点中运算的具体执行者,
Tensor:- 用于存放多维数据的数据结构,方便数据在计算节点之间传递,同时该结构也封装矩阵乘、点积等与矩阵相关的基本操作。
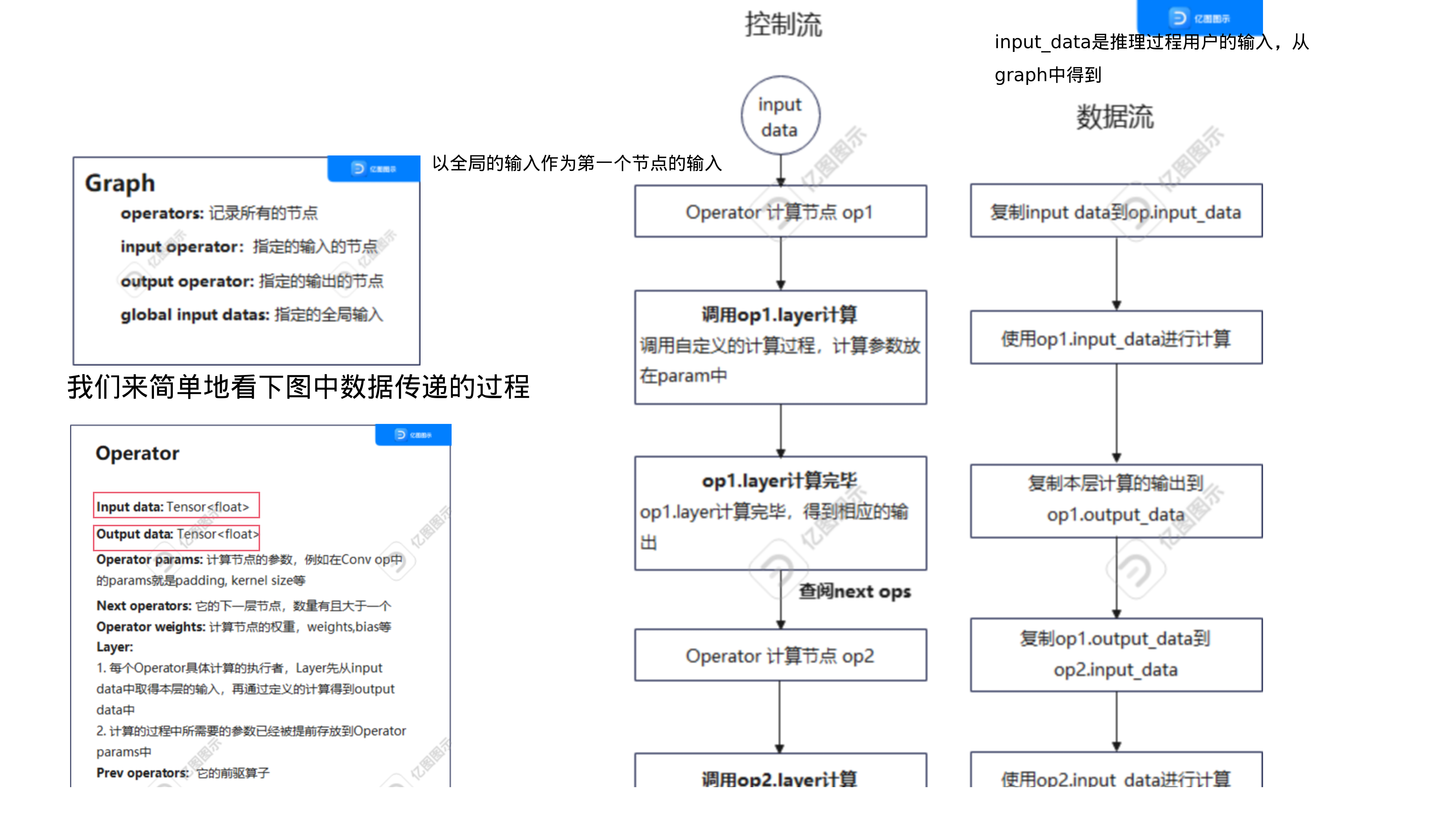
以下的图示是对如上的模块的总结,每个节点都从输入张量input_data中读取数据,并调用该节点对应的Layer计算对应的结果,最后再将结果放入到output_data中。整个计算图第一个节点的输入也是计算图全局的输入,同时,最后一�个节点的输出也是整个计算图的全局输出。
Installation - Linux
01 Docker Init
curl -fsSL get.docker.com -o get-docker.sh
sudo sh get-docker.sh --mirror Aliyun
Docker 即安装完毕,我们只需要启动它并赋予他权限即可
sudo systemctl enable docker
sudo systemctl start docker
sudo chmod 777 /var/run/docker.sock
sudo systemctl restart docker
# validation
docker run hello-world
# output will be like:
Unable to find image 'hello-world:latest' locally
latest: Pulling from library/hello-world
719385e32844: Pull complete
Digest: sha256:fc6cf906cbfa013e80938cdf0bb199fbdbb86d6e3e013783e5a766f50f5dbce0
Status: Downloaded newer image for hello-world:latest
Hello from Docker!
This message shows that your installation appears to be working correctly.
02 Pull Prepared Image
# 拉取Docker镜像
sudo docker pull registry.cn-hangzhou.aliyuncs.com/hellofss/kuiperinfer:datawhale
# 创建本地文件夹,并将课程代码克隆到该文件夹中
mkdir ~/code/kuiperdatawhale
cd ~/code/kuiperdatawhale
git clone https://github.com/zjhellofss/kuiperdatawhale.git
# 创建并运行一个镜像的容器
sudo docker run -it registry.cn-hangzhou.aliyuncs.com/hellofss/kuiperinfer:datawhale /bin/bash
# 在容器中输入ifconfig命令查看ip地址
eth0: flags=4163<UP,BROADCAST,RUNNING,MULTICAST> mtu 1500
inet 172.17.0.4 netmask 255.255.0.0 broadcast 172.17.255.255
ether 02:42:ac:11:00:04 txqueuelen 0 (Ethernet)
RX packets 55 bytes 8479 (8.4 KB)
RX errors 0 dropped 0 overruns 0 frame 0
TX packets 0 bytes 0 (0.0 B)
TX errors 0 dropped 0 overruns 0 carrier 0 collisions 0
尝试使用 ssh 命令连接容器 ssh me@xxx.xxx...
username = me- ip 地址是上方 ipconfig 输出中的 inet
password = 1
KuiperCourse Notes
.vscode/tasks.json
{
"tasks": [
{
"type": "cppbuild",
"label": "C/C++: g++ build active file",
"command": "/usr/bin/g++",
"args": [
"-fdiagnostics-color=always",
"-g",
"${file}",
"-o",
"${fileDirname}/${fileBasenameNoExtension}",
"-lgtest",
"-lgtest_main",
"-lpthread",
"-lblas",
"-larmadillo",
"-lglog"
],
"options": {
"cwd": "${fileDirname}"
},
"problemMatcher": ["$gcc"],
"group": {
"kind": "build",
"isDefault": true
},
"detail": "Task generated by Debugger."
}
],
"version": "2.0.0"
}
01 Unit test & Armadillo
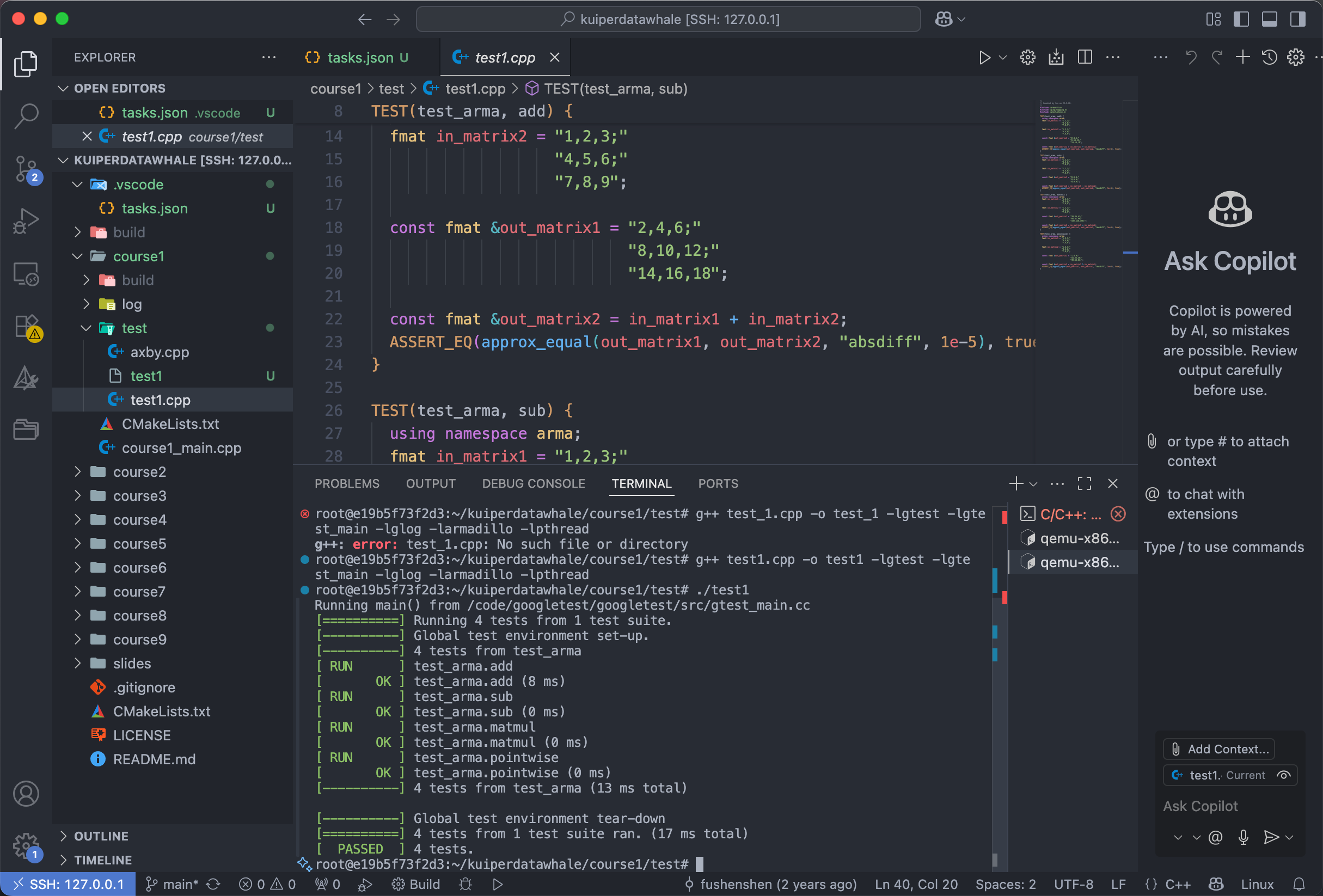
# git clone ...
git fetch origin
git checkout -b first origin/first
mkdir build
cd build
cmake ..
make -j8
# 编译 test_first.cpp
cd test/
g++ test1.cpp -o test1 -lgtest -lgte
st_main -lglog -larmadillo -lpthread
# 运行
./test1
test_add 函数用来测试 armadillo 的矩阵加法接口
TEST(test_arma, add) {
using namespace arma;
fmat in_matrix1 = "1,2,3;"
"4,5,6;"
"7,8,9";
fmat in_matrix2 = "1,2,3;"
"4,5,6;"
"7,8,9";
const fmat &out_matrix1 = "2,4,6;"
"8,10,12;"
"14,16,18";
const fmat &out_matrix2 = in_matrix1 + in_matrix2;
ASSERT_EQ(approx_equal(out_matrix1, out_matrix2, "absdiff", 1e-5), true);
}
test_sub 函数用来测试 armadillo 的矩阵减法接口
TEST(test_arma, sub) {
using namespace arma;
fmat in_matrix1 = "1,2,3;"
"4,5,6;"
"7,8,9";
fmat in_matrix2 = "1,2,3;"
"4,5,6;"
"7,8,9";
const fmat &out_matrix1 = "0,0,0;"
"0,0,0;"
"0,0,0;";
const fmat &out_matrix2 = in_matrix1 - in_matrix2;
ASSERT_EQ(approx_equal(out_matrix1, out_matrix2, "absdiff", 1e-5), true);
}
test_matmul 函数用来测试 armadillo 的矩阵乘法接口
// 测试矩阵乘法 (matrix multiplication)
TEST(test_arma, matmul) {
using namespace arma; // 使用 Armadillo 命名空间,简化写法
// 定义第一个 3x3 矩阵
fmat in_matrix1 = "1,2,3;"
"4,5,6;"
"7,8,9";
// 定义第二个 3x3 矩阵
fmat in_matrix2 = "1,2,3;"
"4,5,6;"
"7,8,9";
// 期望的矩阵乘法结果 (in_matrix1 * in_matrix2)
// 手工计算得出:
// [1*1+2*4+3*7, 1*2+2*5+3*8, 1*3+2*6+3*9] = [30, 36, 42]
// [4*1+5*4+6*7, 4*2+5*5+6*8, 4*3+5*6+6*9] = [66, 81, 96]
// [7*1+8*4+9*7, 7*2+8*5+9*8, 7*3+8*6+9*9] = [102, 126, 150]
const fmat &out_matrix1 = "30,36,42;"
"66,81,96;"
"102,126,150;";
// 实际计算结果:调用 Armadillo 的矩阵乘法运算符 *
const fmat &out_matrix2 = in_matrix1 * in_matrix2;
// 使用 approx_equal 进行比较("absdiff", 1e-5 表示允许的误差范围)
ASSERT_EQ(approx_equal(out_matrix1, out_matrix2, "absdiff", 1e-5), true);
}
02 Tensor 张量
- 张量 Tensor
- 在深度学习的计算中,我们往往采用的是多种多样的矩阵进行运算,而这些矩阵的集合体通常被称为 张量.
- 张量本质是「多维数组」multi-dimensional array
- 形状 Shape
- 维度大小的数组,例如
shape = {channels, rows, cols}
- 维度大小的数组,例如
- 展平 Flatten
- 把多维张量展平为一维向量。
- 填充 Padding
- 给矩阵/��张量边缘补零或者其他值。
对于一个张量类而言,数据将被设计成依次摆放的三维格式,分别是
channels(通道数)rows(行数)cols(列数)
一个张量类主要由以下部分组成:
- 数据本身存储在该类的数据空间中,数据可包括双精度 (
double)、单精度 (float)或整型 (int)。 - 为了处理多维张量数据,需要使用
shape变量来存储张量的维度信息。例如,对于一个维度为3,长和宽均为224的张量,其维度信息可以表示为(3, 224, 224)。 - 张量类中定义了多个类方法,如返回张量的宽度、高度、填充数据和张量变形 (
reshape) 等操作。
张量类的设计
为了更好地满足计算密集型任务的需求,一个张量类不仅需要在软件工程的层面上优化对外接口,还需要提供高效的矩阵相乘等算法实现。尤其是对于深度学习推理等任务来说,高效实现这些算法至关重要。
从头设计一个张量类具有较大的编码难度。在本项目中,我们选择在 arma::fcube三维矩阵 的基础上进行开发。
如下图所示,三维的arma::fcube是由多个二维矩阵matrix(即上一节课中介绍的arma::fmat)沿通道维度叠加得到。
在此基础上,我们的张量类将在叠加而成的三维矩阵arma::fcube的基础上提供扩充和封装,以使其更适用于我们的推理框架项目。
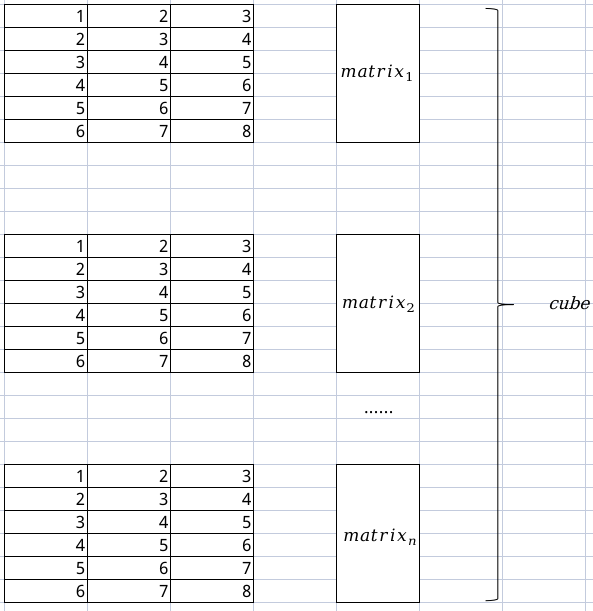
对于这样的 Tensor 类,我们主要做了以下的两个工作:
- 提供对外的接口,对外接口由
Tensor类在fcube类的基础上进行提供,以供用户更好地访问多维数据。 - 封装矩阵相关的计算功能,这样一来不仅有更友好的数据访问和使用方式,也能有高效的矩阵算法实现。
template <>
class Tensor<float> {
public:
uint32_t rows() const;
uint32_t cols() const;
uint32_t channels() const;
uint32_t size() const;
void set_data(const arma::fcube& data);
...
...
...
private:
std::vector<uint32_t> raw_shapes_; // 张量数据的实际尺寸大小
arma::fcube data_; // 张量数据
};
以下的每一个矩阵都是4行3列大小的�矩阵,即4 x 3 矩阵。上文提到,一个三维矩阵(arma::fcube)是由多个二维矩阵沿着通道维度叠加而成的。因此,以下的三维矩阵fcube的形状为(3, 4, 3),数据分布如下图所示:
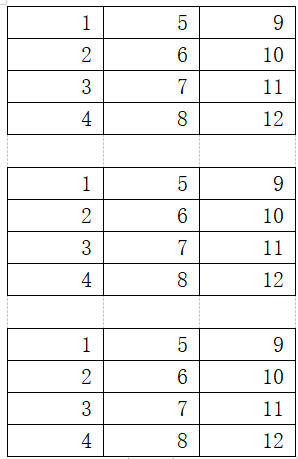
有了张量的形状认知,下一步就是思考如何将数据存入到各式各样的的张量数据之中,不同的存放顺序很可能会对我们的计算过程造成影响。
数据的摆放顺序
矩阵存储有两种形式:
- 行主序 Row-major order
- 含义:一行的数据是连续存储的。
- 常见语言:C/C++ 默认(例如
std::vector<vector<int>>或 C 数组)。 - NumPy 默认也是 row-major(除非 order='F')。
- 内存布局:
[a00, a01, a02, a10, a11, a12, ...]
- 列主序 Column-major order
- 含义:一列的数据是连续存储的。
- 常见语言:Fortran、MATLAB、Armadillo 默认使用列主序。
- 内存布局:
[a00, a10, a20, a01, a11, a21, ...]
行主序
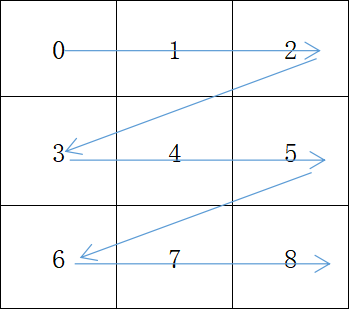
对于一组数据,在矩阵中如果按行摆放,直到该行摆满后再到下一行摆放,并以此类推。这种存储数据的方式被称为行主序 Row-major order.
假如我们现在 有一组数据的值是0到8,这9个数据在一个行主序的 3 x 3 矩阵中有如下的排布形式,其中箭头指示了内存地址的增长方向。从图中可以看出,内存地址增长的方向先是横向,然后是纵向,呈Z字形。
列主序
对于一组数据,在矩阵中如果依次存放顺序是先摆满一列,将剩余的数据依次存放到下一列,并以此类推。按照这种方式摆放的形式被称为列主序 Column-major order.
同理,我们现在有9个数据,依次为0到8,将它摆放到一个列主序 3 x 3 的矩阵当中,并有如下的形式,其中箭头指示了内存地址的增长方向。
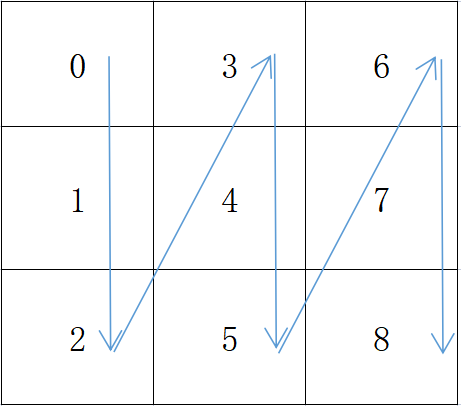
从图中可以看出 channels 内存地址增长的方向先是纵向,然后是横向,呈倒Z字形。在 armadillo 中默认的顺序就是列主序的. 而 Pytorch 张量默认顺序是行主序的,所以我们在程序中需要进行一定适应和调整。
03 Computational Graph 计算图
计算图的概念
KuiperInfer 使用的模型格式是 PNNX.
PNNX是PyTorch Neural Network Exchange的缩写,其愿景��是能够将PyTorch模型文件直接导出为高效、简洁的计算图。计算图包括了以下几个部分,作为一种计算图形式,PNNX自然也不例外,正如第一章所述:
Operator: 深度学习计算图中的计算节点。Graph: 有多个Operator串联得到的有向无环图,规定了各个计算节点(Operator)执行的流程和顺序。Layer: 计算节点中运算的具体执行者,Layer类先读取输入张量中的数据,然后对输入张量进行计算,得到的结果存放到计算节点的输出张量中,当然,不同的算子中Layer的计算过程会不一致。Tensor: 用于存放多维数据的数据结构,方便数据在计算节点之间传递,同时该结构也封装矩阵乘、点积等与矩阵相关的基本操作。
PNNX 计算图的优势
以往我们将训练好的模型导出为 ONNX 结构之后,模型中的一个复杂算子不仅经常会被拆分成多个细碎的算子,而且为了将这些细碎的算子拼接起来完成原有算子的功能,通常还需要一些称之为“胶水算子”的辅助算子,例如 Gather 和 Unsqueeze 等。
你还认得出下图的算子,其实是被拆分后 LayerNorm 算子吗?当然 ONNX 使用多个小算子去组合、等价一个复杂算子的设计,也是为了用尽可能少的算子去兼容更多的训练框架。
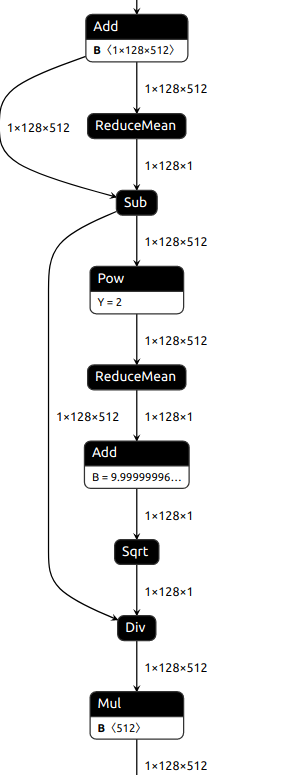
但是过于细碎的计算图会不仅不利于推理的优化。另外,拆分的层次过于细致,也会导致算法工程师难以将导出的模型和原始模型进行结构上的相互对应。为了解决以上说到的问题,我们选用 NCNN 推理框架的计算图格式之一 PNNX,你可以在这张图中很直观的看出 PNNX 与 TorchScript 和 ONNX 的区别:
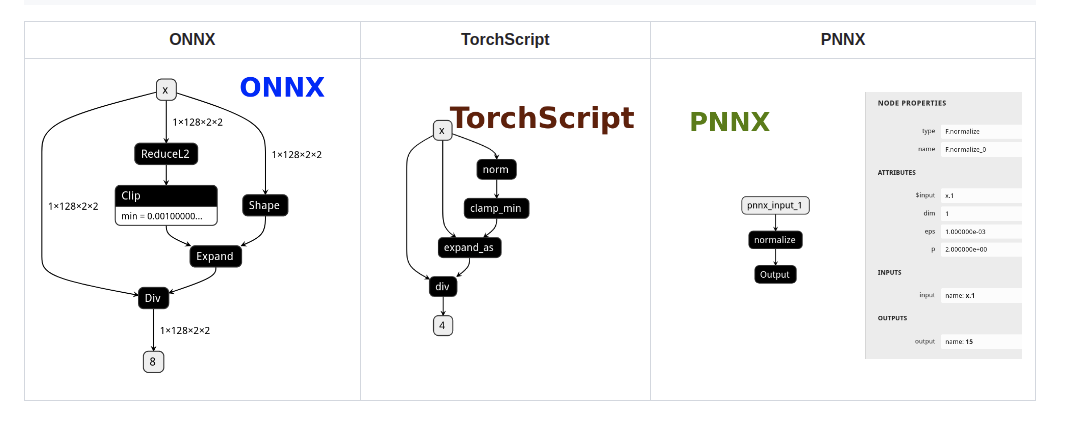
那么 PNNX 给我们带来了什么呢?下图是它在模型部署中的位置,可以看到,一个模型文件从 PyTorch 先经历了 TorchScript 的导出,随后再经过 PNNX 的优化得到最终的模型文件(无视最后导出为 NCNN 的部分)。
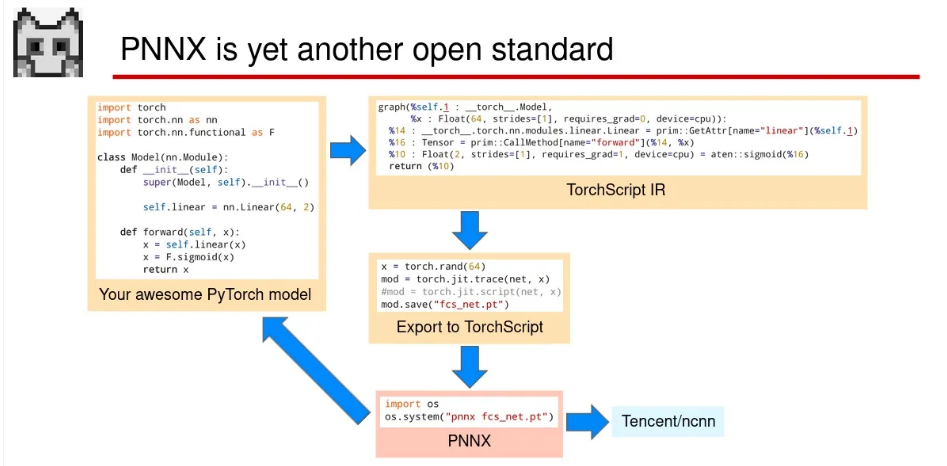
-
使用模板匹配(
pattern matching)的方法将匹配到的子图用对应等价的大算子替换掉,例如可以将上图子图中的多个小算子(可能是在TorchScript中被拆分的)重新替换为LayerNorm算子。或者在对PyTorch模型导出时,也可以自定义某个nn.Module不被拆分; -
在
PyTorch中编写的简单算术表达式在转换为PNNX后,会保留表达式的整体结构,而不会被拆分成许多小的加减乘除算子。例如表达式add(mul(@0, @1),add(@2, @3))不会被拆分为两个add算子和一个mul算子,而是会生成一个��表达式算子Expression; -
PNNX项目中有大量图优化的技术,包括了算子融合,常量折叠和消除,公共表达式消除等技术。- 算子融合优化是一种针对深度学习神经网络的优化策略,通过将多个相邻的计算算子合并为一个算子来减少计算量和内存占用。以卷积层和批归一化层为例,我们可以把两个算子合并为一个新的算子,也就是将卷积的公式带入到批归一化层的计算公式中:
# Conv + BN 简化(纯文本版)
# 约定:
# x: 输入
# w: 卷积权重
# b: 卷积偏置
# gamma, beta: BN 的缩放/平移参数
# mu, var: BN 的均值/方差(推理时用运行均值/方差)
# eps: 极小正数,避免除零
# 原始形式
Conv: y = w * x + b
BN: z = gamma * ( (y - mu) / sqrt(var + eps) ) + beta
# 融合到单个卷积(Fuse)
w_fused = gamma / sqrt(var + eps) * w
b_fused = gamma / sqrt(var + eps) * (b - mu) + beta
# 融合后的前向
y_fused = w_fused * x + b_fused-
常量折叠是将在编译时期间将表达式中的常量计算出来,然后将结果替换为一个等价的常量,以减少模型在运�行时的计算量。
-
常量移除就是将计算图中不需要的常数(计算图推理的过程中未使用)节点删除,从而减少计算图的文件和加载后的资源占用大小。
-
公共表达式消除优化是一种针对计算图中重复计算的优化策略,它可以通过寻找并合并重复计算的计算节点,减少模型的计算量和内存占用。公共子表达式检测是指查找计算图中相同的子表达式,公共子表达式消除是指将这些重复计算的计算节点合并为一个新的计算节点,从而减少计算和内存开销。举个例子
X = input(3,224,224)
A = Conv(X)
B = Conv(X)
C = A + B在上方的代码中,
Conv(X)这个结果被计算了两次,公共子表达式消除可以将它优化为如下代码,这样一来就少了一次卷积的计算过程。X = input(3,224,224)
T = Conv(X)
C = T + T
综上所述,如果在我们推理框架的底层用PNNX计算图,就可以吸收图优化和算子融合的结果,使得推理速度更快更高效。
PNNX 计算图的格式
PNNX 由图结构 (Graph), 运算符 (Operator)和操作数 (Operand)这三种结构组成的,设计非常简洁。
用于测试的 PyTorch 模型
为了帮助同学们更好地掌握计算图格式,我们准备了一对较小的模型文件 linear.param 和 linear.bin 来做单步调试,它们分别是网络的结构定义和权重文件。该模型在 PyTorch 中的定义如下
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear = nn.Linear(32, 128)
def forward(self, x):
x = self.linear(x)
x = F.sigmoid(x)
return x
这是一个非常简单的模型,其作用是对输入 x 进行线性映射(从32维到128维),并对输出进行 sigmoid 计算,从而得到最终的计算结果。该模型的网络结构如下图所示(使用 Netron 软件打开 linear.param),我们以其中的 Linear 层为例
Netron: https://netron.app/
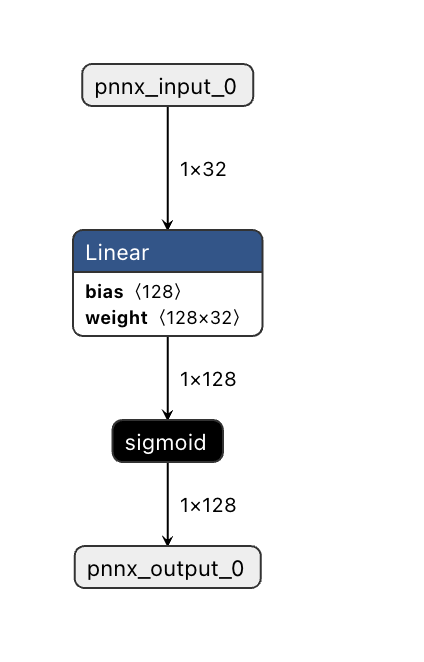
Linear层有#0和#1两个操作数,分别为输入和输出张量,形状依次为(1, 32)和(1, 128);Linear层有两个属性参数:@weight和@bias,用于存储该层的权重数据信息,分别对应权重(即weight)和偏置(即bias)。可以看到这两个权重的形状分别为(1, 32)和(1, 128),在后续过程中可以根据需要进行权重加载。Linear层有三个属性:bias,in_features和out_features,分别表示是否使用偏置项、线性连接层的输入维度和输出维度。
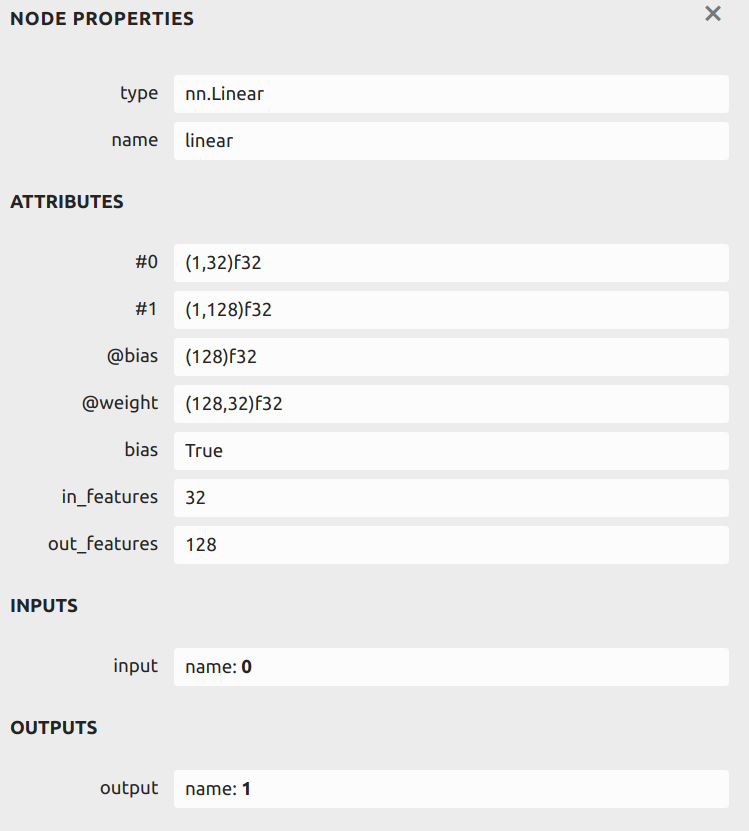
PNNX 中的图结构 Graph
// 计算图:管理算子(Operator)与张量/边(Operand)的关系与顺序
// 说明:这里使用裸指针,通常由 Graph 统一创建/销毁(或改用智能指针以避免泄漏)
class Graph {
public:
// 新建一个算子;type:算子类型(如 "Convolution"、"Relu"),name:全局唯一名
// 返回新算子的指针
Operator* new_operator(const std::string& type, const std::string& name);
// 在已有算子 cur 之前插入一个新算子(用于重排或在中间加节点)
Operator* new_operator_before(const std::string& type, const std::string& name, const Operator* cur);
// 基于 TorchScript 的 IR 值创建一个操作数/张量(与导入的 JIT 图对应)
Operand* new_operand(const torch::jit::Value* v);
// 以名字创建一个操作数/张量(适合常量或命名中间结果)
Operand* new_operand(const std::string& name);
// 按名字查找已存在的操作数;未找到通常返回 nullptr
Operand* get_operand(const std::string& name);
// 图中的所有算子;通常按构建/拓扑顺序存放
std::vector<Operator*> ops;
// 图中的所有操作数/张量
std::vector<Operand*> operands;
};
Graph 的核心作用是管理计算图中的运算符和操作数。下面我们将对这两个概念进行说明
Operator类用来表示计算图中的运算符 aka 算子,比如一个模型中的Convolution,Pooling等算子;Operand类用来表示计算图中的操作数,即与一个运算符有关的输入和输出张量;Graph类的成员函数提供了方便的接口用来创建和访问操作符和操作数,以构建和遍历计算图。同时,它也是模型中运算符(算子)和操作数的集合。
PNNX 中图结构相�关的单元测试
TEST(test_ir, pnnx_graph_ops) {
using namespace kuiper_infer;
/**
* 本用例:加载 PNNX 导出的计算图文件(.param + .bin),
* 并打印图中所有算子(op)的名称,验证能否正确解析。
*/
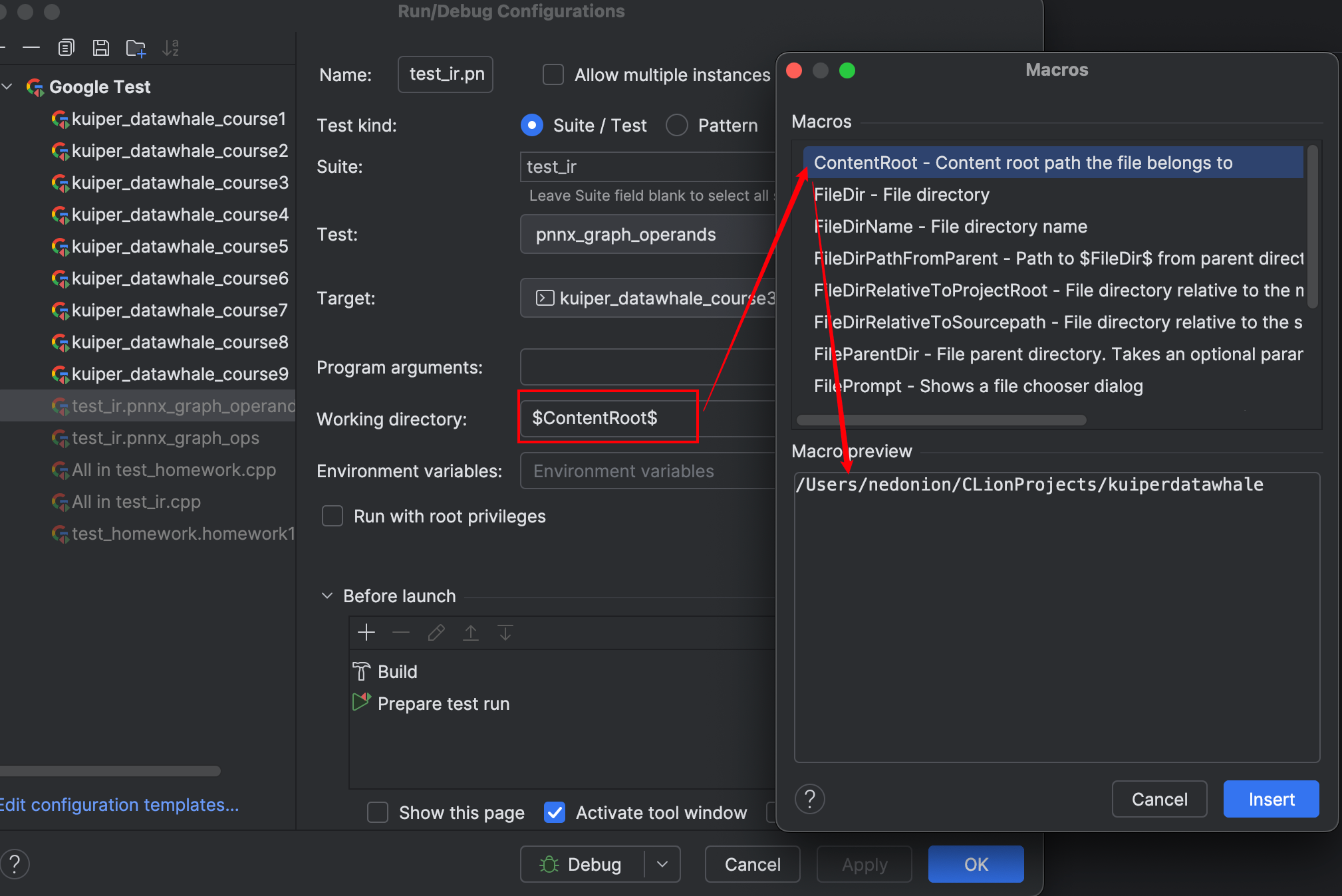
// 注意:相对路径是相对于“当前运行目录”(working directory)
// 比如在 build/ 下运行测试,路径需能从 build/ 定位到课程资源目录
std::string bin_path("course3/model_file/test_linear.pnnx.bin");
std::string param_path("course3/model_file/test_linear.pnnx.param");
// 创建 pnnx::Graph 对象(unique_ptr 管理生命周期,避免内存泄漏)
std::unique_ptr<pnnx::Graph> graph = std::make_unique<pnnx::Graph>();
// 读取/反序列化图:返回 0 表示成功,非 0 表示失败(通常是找不到文件或格式错误)
int load_result = graph->load(param_path, bin_path);
// 如果断言失败,优先检查相对路径是否正确(param_path / bin_path)
ASSERT_EQ(load_result, 0);
// graph->ops 为图中所有算子(Operator*)的列表
const auto &ops = graph->ops;
// 逐个输出算子名称,验证图结构是否被成功解析
for (int i = 0; i < ops.size(); ++i) {
LOG(INFO) << ops.at(i)->name;
}
}
PNNX 中的运算符结构 Operator
我们来聊聊PNNX中的运算符结构。
class Operator {
public:
std::vector<Operand*> inputs;
std::vector<Operand*> outputs;
std::string type;
std::string name;
std::vector<std::string> inputnames;
std::map<std::string, Parameter> params;
std::map<std::string, Attribute> attrs;
};
在PNNX中,Operator用来表示一个算子,它由以下几个部分组成:
inputs: 类型为std::vector<Operand*>, 表示这个算子在计算过程中所需要的输入操作数Operand;outputs: 类型为std::vector<Operand*>, 表示这个算子在计算过程中得到的输出操作数Operand;type和name类型均为std::string, 分别表示该运算符号的类型和名称;params: 类型为std::map, 用于存放该运算符的所有参数(例如卷积运算符中的params中将存放stride,padding,kernel size等信息);attrs: 类型为std::map, 用于存放该运算符所需要的具体权重属性(例如卷积运算符中的attrs中就存放着卷积的权重和偏移量,通常是一��个float32数组)。
PNNX 中的操作数结构 Operand
class Operand {
public:
void remove_consumer(const Operator* c);
Operator* producer;
std::vector<Operator*> consumers;
int type;
std::vector<int> shape;
std::string name;
std::map<std::string, Parameter> params;
};
- 重点值得分析的是操作数结构中的
producer和consumers, 分别表示产生这个操作数的算子和使用这个操作数的算子。 - 值得注意的是产生这个操作数的算子只能有一个,而使用这个操作数的算子可以有很多个。
Kuiper 对计算图的封装
为了更好的使用底层PNNX计算图,我们会在项目中对它进行再次封装,使得PNNX更符合我们的使用需求。
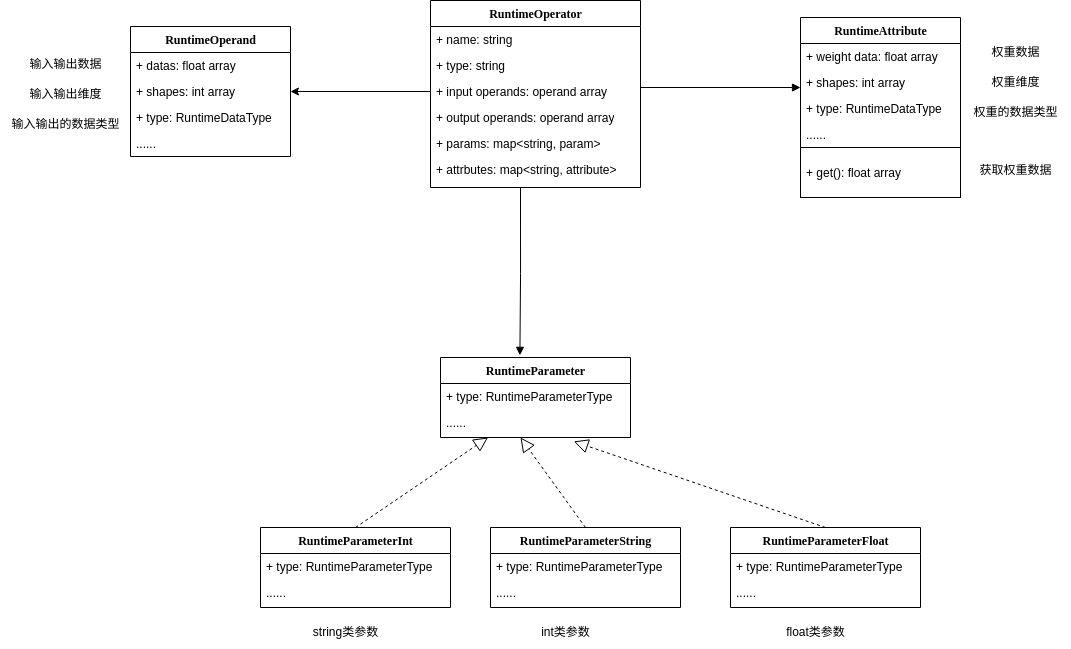
Operator 封装
不难从上图看出,RuntimeOperator 是 Kuiper 计算图中的核心数据结构,是对 PNNX::Operator 的再次封装,它有如下的定义
/**
* @brief 运行时图里的“算子节点”(执行单元)的最小封装
* @details
* 设计要点:
* 1) 该结构既承担“拓扑节点”的角色(上下游连线、输入输出操作数),
* 也承载“执行载体”的角色(Layer + 参数/属性)。
* 2) 成员里大量使用 shared_ptr 而不是裸对象/unique_ptr,原因:
* - 节点与操作数/权重在图内天然存在“多处持有”的需求(例如同一输出被多个下游消费),
* 用 shared_ptr 可简单表达共享所有权,避免复杂的所有权转移。
* - 初始化阶段与执行阶段可能分离,shared_ptr 便于跨阶段/跨模块传递与缓存。
* 3) 少数位置采用原始指针(params),是基于“多态层级 + 轻量对象池/工厂”的传统写法;
* 若需更强的异常安全/RAII,建议后续演进为 unique_ptr 或自定义智能指针。
*/
struct RuntimeOperator {
/**
* @brief 虚析构函数
* @details
* - 该类型作为“多态基”,外界可能以基类指针持有(如 Operator* 指向派生类)。
* - 虚析构确保经基类指针 delete 时,派生类析构能被正确调用,避免资源泄漏。
* - 若仅作为“纯 POD 容器”,也可非虚;但考虑到 Layer 为多态、未来可能派生扩展,保留 virtual 更稳妥。
*/
virtual ~RuntimeOperator();
/**
* @brief 节点是否已执行过 forward(前向计算)
* @details
* - 执行期状态位:避免重复计算,或用于跨批次/流水线的简单去重。
* - 若执行计划更复杂(多流/并行),应配合调度器中的拓扑就绪计数使用。
*/
bool has_forward = false;
/**
* @brief 计算节点名称(唯一标识)
* @details
* - 用作 operators_maps 的 key、日志可读性、调试定位。
* - 唯一性通常由上游图导出工具(PNNX)保证。
*/
std::string name;
/**
* @brief 计算节点类型(如 "Conv", "ReLU", "MatMul"...)
* @details
* - 在构建 Layer 时进行分发(factory/registry)。
* - 也可供可视化/统计用途。
*/
std::string type;
/**
* @brief 节点对应的可执行算子实现(策略对象)
* @details
* - shared_ptr 原因:Layer 可能被图的不同视图/执行上下文共享引用;
* 或不同阶段(初始化/执行/调试)持有同一 Layer 的引用。
* - 若确定 Layer 只会被该节点唯一持有,且无跨结构共享,可用 unique_ptr 简化所有权。
*/
std::shared_ptr<Layer> layer;
/**
* @brief 下游消费者(节点名列表)
* @details
* - 仅保存“名字”,而非直接保存指针引用,有两点考虑:
* (1) 初始化时可先不强绑定指针,降低构建顺序/生命周期耦合;
* (2) 日志/调试更直观(名字可打印)。
* - 若在执行期需要 O(1) 访问下游节点指针,可配合 output_operators 做二阶段解析。
* - 容器选择:vector 保留原始顺序,遍历代价 O(k),k 为扇出数。
*/
std::vector<std::string> output_names;
/**
* @brief 节点的“输出操作数”
* @details
* - 大多数算子只有一个主输出,用一个 shared_ptr 即可表达。
* - 若未来要支持多输出(如 Tuple/Branch),可以演进为 vector<shared_ptr<RuntimeOperand>>。
* - shared_ptr 的原因:
* - 一个输出可能被多个下游节点消费(扇出>1),需要共享持有;
* - 输出张量/Tensor 可能延迟分配或在图优化中被替换(别名/内存复用)。
*/
std::shared_ptr<RuntimeOperand> output_operands;
/**
* @brief 以“上游节点名”为 key 的输入操作数映射
* @details
* - map 的动机:
* - 便于按“上游节点名”直接索引,适合在连线/调试时通过名字查找;
* - 插入/查找为 O(log n),n 为输入个数;输入一般较少,可接受。
* - 也可替换为 unordered_map 获得均摊 O(1) 查找(需权衡可重现性与迭代有序性)。
* - value 使用 shared_ptr 的原因:
* - 输入操作数(RuntimeOperand)可能同时出现在“按名索引 map”
* 与“按序容器 input_operands_seq”里,需要共享所有权。
*/
std::map<std::string, std::shared_ptr<RuntimeOperand>> input_operands;
/**
* @brief 按 PNNX/模型原始顺序排列的输入操作数序列
* @details
* - vector 的动机:需要位置语义(第 i 个输入),forward 阶段按序取更高效。
* - 与 input_operands(map)是同一批 RuntimeOperand 的不同“视图”,
* 二者共享同一批 shared_ptr,避免重复分配与生命周期分裂。
*/
std::vector<std::shared_ptr<RuntimeOperand>> input_operands_seq;
/**
* @brief 下游“名字 -> 节点指针”的快速映射
* @details
* - 与 output_names 对应的二阶段解析结果(把名字解析为指针),
* 便于执行期快速迭代下游��节点,无需再去全局哈希表查找。
* - 使用 map 的原因同上;若更在意均摊 O(1),可换 unordered_map。
* - 使用 shared_ptr 的原因:
* - 拓扑里节点彼此交叉引用,shared_ptr 能表达共享所有权;
* - 若担心循环引用,可将某一侧改为 weak_ptr(例如下游列表持 weak_ptr)。
*/
std::map<std::string, std::shared_ptr<RuntimeOperator>> output_operators;
/**
* @brief 算子的参数(标量/数组/字符串等超参数)
* @details
* - 使用原始指针(RuntimeParameter*)的历史原因:
* - 常见于“轻量参数对象 + 工厂创建 + 统一销毁”的模式;
* - 避免为每种派生类型套智能指针模板(老代码里常见)。
* - 风险与改进:
* - 需要明确谁负责 delete(通常由 RuntimeOperator 或图在析构时遍历释放);
* - 若追求异常安全与资源确定释放,建议升级为
* std::unique_ptr<RuntimeParameter> 或��使用自定义删除器的 std::shared_ptr。
* - 容器选型为 map:
* - 参数通常以“字符串键(如 kernel_size, stride)”索引,map 直观且顺序稳定;
* - 也可用 unordered_map 换取更快的平均查找。
*/
std::map<std::string, RuntimeParameter*> params;
/**
* @brief 算子的属性(多为权重/常量张量)
* @details
* - shared_ptr 的原因:
* - 权重可能被算子副本/不同执行上下文共享引用(如多流/复用);
* - 构图优化(常量折叠/共享权重)时,引用计数能自然管理生命周期。
* - key 使用字符串(如 "weight", "bias"),与导出工具/Layer 实现对齐。
* - 若权重很大且不会共享,也可 unique_ptr;但一旦发生多处持有场景,需要回到 shared_ptr。
*/
std::map<std::string, std::shared_ptr<RuntimeAttribute>> attribute;
};
以上这段代码定义了一个名为 RuntimeOperator 的结构体。结构体包含以下成员变量
name: 运算符节点的名称,可以用来区分一个唯一节点,例如Conv_1,Conv_2等;type: 运算符节点的类型,例如Convolution,Relu等类型;layer: 负责完成具体计算的组件,例如在Convolution Operator中,layer对输入进行卷积计算,即计算其相应的卷积值;input_operands和output_operands分别表示 该运算符的输入和输出操作数。- 如果一�个运算符(
RuntimeOperator)的输入大小为(4, 3, 224, 224),那么在input_operands变量中,datas数组的长度为 4,数组中每个元素的张量大小为(3, 224, 224). params: 是运算符RuntimeOperator的参数信息,包括卷积层的卷积核大小、步长等信息。attribute: 是运算符RuntimeOperator的权重、偏移量信息,例如Matmul层或Convolution层需要的权重数据
初始化 PNNX 操作数 Operand 到 RuntimeOperand
/**
* @brief 初始化运行时图
* @return true:成功;false:失败(已通过 LOG 输出原因)
* @details
* 加载流程(关键步骤):
* 1) 基本校验:param/bin 路径非空
* 2) 解析 PNNX Graph(graph_->load)
* 3) 遍历 PNNX Operator 列表,逐个构建 RuntimeOperator:
* - name/type
* - 输入:根据 Operand->producer 连接拓扑
* - 输出:记录下游消费者名字(仅保存名字,实际指针连线可延后)
* - 属性 attrs:多为权重(float32/shape/data)
* - 参数 params:标量/数组/字符串等
*
* 错误处理:
* - 任一步失败均返回 false 并写 ERROR/FATAL 日志
*
* 复杂度:
* - 假设算子数为 N,边数为 E,整体为 O(N + E)
*
* 注意:
* - 当前未执行“拓扑排序”,operators_ 顺序为 PNNX 的原始顺序
* - 若后续执行阶段需要拓扑序,请在 Init 末尾新增排序步骤
*/
bool RuntimeGraph::Init() {
// 1) 基本路径校验
if (this->bin_path_.empty() || this->param_path_.empty()) {
LOG(ERROR) << "The bin path or param path is empty";
return false;
}
// 2) 创建并加载 PNNX Graph(所有权:std::unique_ptr 自动管理)
this->graph_ = std::make_unique<pnnx::Graph>();
int load_result = this->graph_->load(param_path_, bin_path_);
if (load_result != 0) {
LOG(ERROR) << "Can not find the param path or bin path: " << param_path_
<< " " << bin_path_;
return false;
}
// 3) 取出算子列表并做基本校验
std::vector<pnnx::Operator *> operators = this->graph_->ops;
if (operators.empty()) {
LOG(ERROR) << "Can not read the layers' define";
return false;
}
// 4) 清空旧数据(保证可重复 Init)
this->operators_.clear();
this->operators_maps_.clear();
// 5) 遍历 PNNX Operator,构建 RuntimeOperator
for (const pnnx::Operator *op: operators) {
if (!op) {
// 防守式:跳过空指针节点
LOG(ERROR) << "Meet the empty node";
continue;
} else {
// 5.1 创建运行时算子(共享所有权,便于图内多处引用)
std::shared_ptr<RuntimeOperator> runtime_operator =
std::make_shared<RuntimeOperator>();
// 5.2 基本元数据
runtime_operator->name = op->name; // 唯一标识
runtime_operator->type = op->type; // 算子类型(如 Conv/Relu 等)
// 5.3 解析输入(根据 Operand->producer 建立“上游到我”的连线信息)
const std::vector<pnnx::Operand *> &inputs = op->inputs;
if (!inputs.empty()) {
InitGraphOperatorsInput(inputs, runtime_operator);
}
// 5.4 解析输出(记录下游消费者名称,便于后续连线或调度)
const std::vector<pnnx::Operand *> &outputs = op->outputs;
if (!outputs.empty()) {
InitGraphOperatorsOutput(outputs, runtime_operator);
}
// 5.5 解析属性 attrs(通常是权重):类型、shape、原始二进制
const std::map<std::string, pnnx::Attribute> &attrs = op->attrs;
if (!attrs.empty()) {
InitGraphAttrs(attrs, runtime_operator);
}
// 5.6 解析参数 params(标量/数组/字符串):执行期的可配置超参数
const std::map<std::string, pnnx::Parameter> ¶ms = op->params;
if (!params.empty()) {
InitGraphParams(params, runtime_operator);
}
// 5.7 注册到容器与索引(名字->指针)
this->operators_.push_back(runtime_operator);
this->operators_maps_.insert({runtime_operator->name, runtime_operator});
}
}
// 提示:如需在此处做拓扑排序,可新增对 operators_ 的重排
return true;
}
RuntimeOperand 设计理念
- 作用定位
RuntimeOperand用来描述计算图中算子之间传递的数据张量,即节点的输入/输出。不同于RuntimeAttribute(存储固定权重),它代表的是运行时动态数据。
- 封装内容
- name:操作数的唯一标识,用于在算子之间建立连接关系。
- shapes:张量形状(如
[batch, channels, height, width]),推理过程中可动态变化(如 batch_size 可变)。 - datas:真正存放数据的容器,是
std::vector<std::shared_ptr<Tensor<float>>>,支持 batch 或多张量场景。 - type:数据类型(目前主要是 float32,未来可扩展到 int8/FP16 等)。
- 设计要点:
datas设计成 vector of Tensor,是为了支持- Mini-batch 输入(一个 Operand 里存多条样本数据);
- 算子输出多个结果时按序存放。
- 使用
shared_ptr<Tensor<float>>保证数据能在多个算子之间安全共享,避免不必要的拷贝。 - 与
RuntimeAttribute的区别RuntimeAttribute是静态参数(权重/常量),加载后固定;RuntimeOperand是动态变量,在推理时不断被更新和传递。
- 典型使用场景
- Conv 节点的输入 Operand 保存输入特征图,输出 Operand 保存卷积结果。
- BN 节点的输入 Operand 来自 Conv 输出,经过归一化后再作为下一个算子的输入。
- 多输入算子(如 Add、Concat)会有多个 RuntimeOperand,按顺序排列。
/// 计算图节点的输入/输出操作数
/// @note
/// - 表示算子之间传递的数据张量(运行时变量,而非固定权重)
/// - 可同时用于输入和输出,取决于所在算子的上下文
struct RuntimeOperand {
std::string name; ///< 操作数名称,用于建立算子之间的连接关系
std::vector<int32_t> shapes; ///< 张量形状,例如 {batch, channels, height, width}
/// 操作数对应的数据
/// - 使用 vector 是为了支持 batch 或多张量输出
/// - 使用 shared_ptr 避免在多个算子之间传递时发生不必要拷贝
std::vector<std::shared_ptr<Tensor<float>>> datas;
/// 操作数的数据类型
/// - 一般是 float32
/// - 保留枚举字段便于未来扩展 INT8/FP16 等类型
RuntimeDataType type = RuntimeDataType::kTypeUnknown;
};
初始化 PNNX 权重到 RuntimeAttribute
/**
* @brief 初始化图算子的属性(通常是权重/常量)
* @param attrs 属性列表(PNNX 的 Attribute 字典)
* @param runtime_operator 运行时算子
* @details
* - 目前仅支持 attr.type == 1 (float32 权重),并保存��:
* type(kTypeFloat32) / weight_data(原始字节) / shape(维度信息)
* - 若未来需要支持 INT8/FP16/BF16/稀疏权重等,请在此扩展类型映射
* - 所有权:权重数据拷贝到 RuntimeAttribute::weight_data(std::vector<uint8_t>)
*/
void RuntimeGraph::InitGraphAttrs(
const std::map<std::string, pnnx::Attribute> &attrs,
const std::shared_ptr<RuntimeOperator> &runtime_operator) {
for (const auto &[name, attr]: attrs) {
switch (attr.type) {
case 1: {
std::shared_ptr<RuntimeAttribute> runtime_attribute =
std::make_shared<RuntimeAttribute>();
runtime_attribute->type = RuntimeDataType::kTypeFloat32;
runtime_attribute->weight_data = attr.data; // 二进制拷贝
runtime_attribute->shape = attr.shape; // 维度信息
runtime_operator->attribute.insert({name, runtime_attribute});
break;
}
default: {
// 其它类型暂不支持;若 PNNX 侧新增类型,需在此同步实现
LOG(FATAL) << "Unknown attribute type: " << attr.type;
}
}
}
}
我们需要依次将每个 Operand 中的数据搬运到新初始化的 RuntimeOperand 中,包括 type, name, shapes 等信息,并记录输出这个操作数 Operand 的运算符 producer.
搬运完成后,再将数据完备的 RuntimeOperand 插入到待初始化的 RuntimeOperator 中。
RuntimeAttribute 设计理念
- 核心作用
RuntimeAttribute专门用来存储算子的权重参数或常量张量,不同于运行时输入输出,它们通常在模型加载时就固定,不随推理过程变化。
- 封装内容: 每个
RuntimeAttribute包含三类核心信息- 原始字节数据(
weight_data):以std::vector<char>存储,保证能兼容不同精度类型(float32、int8、bf16 等); - 张量形状(
shape):如{64, 3, 7, 7}表示卷积核; - 数据类型(
type):通过枚举标记精度,确保在读取时做正确的解释。
- 原始字节数据(
- 延迟解析的好处
- 数据在内存中保持原始字节形式,只有在算子真正需要时才转换为目标类型,例如
- 卷积权重:
auto w = attr.get<float>(); - 量化权重:
auto w = attr.get<int8_t>(); - 这样既能避免重复拷贝,又能适配不同算子需求。
- 卷积权重:
- 数据在内存中保持原始字节形式,只有在算子真正需要时才转换为目标类型,例如
- 内存优化: 在权重被上传到 GPU/专用加速器后,可以调用
ClearWeight()清空 CPU 端数据,释放内存。例如:- 在显存充足的 GPU 推理中,可以直接保留原始数据;
- 在移动端或嵌入式设备上,上传后清理 CPU 内存能显著减少内存占用。
- 典型场景举例
- 卷积层(Conv):存储
weight(形状[out_channels, in_channels, kH, kW])、bias(形状[out_channels]); - BatchNorm 层(BN):存储
running_mean、running_var、gamma、beta; - 全连接层(Linear/FC):存储
[out_features, in_features]的权重矩阵; - Embedding:存储
vocab_size × embedding_dim的查找表。
- 卷积层(Conv):存储
- 扩展性: 当前实现仅支持基本类型(float32),但接口设计允许未来扩展到更多数据格式
- 低精度推理 INT8、FP16、BF16.
- 稀疏权重存储 CSR、COO 格式.
- 混合精度场景 部分层 FP16,部分层 FP32.
/// 计算图节点的属性信息(如权重、偏置等常量)
struct RuntimeAttribute {
/// 原始权重数据(二进制字节形式存储,延迟解析为具体类型)
std::vector<char> weight_data;
/// 权重张量的形状,例如 {64, 3, 7, 7}
std::vector<int> shape;
/// 权重数据类型(float32/int8...),默认 Unknown
RuntimeDataType type = RuntimeDataType::kTypeUnknown;
/**
* @brief 转换为指定类型的权重数组
* @param need_clear_weight 是否在读取后清空 weight_data
*/
template <class T>
std::vector<T> get(bool need_clear_weight = true);
/// 清空权重数据以释放内存
void ClearWeight();
};
初始化 PNNX 参数到 RuntimeParam
- 遍历 PNNX 参数字典
params(每个参数有名字和类型)。 - 根据参数类型创建对应的运行时参数对象
- int →
RuntimeParameterInt - float →
RuntimeParameterFloat - bool →
RuntimeParameterBool - string →
RuntimeParameterString - 数组 →
RuntimeParameterIntArray/FloatArray/StringArray - 未知 → 创建占位对象
- int →
- 把新建对象插入到
runtime_operator->params,以参数名为 key。 - 如果遇到不支持的类型,直接报错退出。
/**
* @brief 初始化图算子的参数
* @param params 参数列表(PNNX 的参数字典,key = 参数名,value = 参数对象)
* @param runtime_operator 运行时算子(目标对象,将填充其 params 字典)
* @details
* - 功能:将 PNNX 导出的通用 Parameter(多类型)解析为运行时框架内部的 RuntimeParameter 对象。
* - 存储方式:
* - runtime_operator->params 是一个 map<string, RuntimeParameter*>,
* key 是参数名(如 "kernel_size", "stride"),value 是一个堆上分配的 RuntimeParameter 派生类对象。
* - 使用原始指针是为了避免在基类中做模板化(简化继承体系),
* 但意味着需要在 RuntimeOperator 析构时统一释放这些对象,避免内存泄漏。
* - 参数类型覆盖:
* - Unknown -> RuntimeParameter (占位符,用于未识别参数)
* - Bool -> RuntimeParameterBool (布尔值,如 "bias" 开关)
* - Int -> RuntimeParameterInt (单个整数,如 "groups")
* - Float -> RuntimeParameterFloat (单个浮点数,如 "epsilon")
* - String -> RuntimeParameterString (字符串,如 "padding_mode")
* - IntArray -> RuntimeParameterIntArray (整数数组,如 "kernel_size = [3,3]"�)
* - FloatArray -> RuntimeParameterFloatArray (浮点数组,如 "mean=[0.5,0.5,0.5]")
* - StringArray -> RuntimeParameterStringArray (字符串数组,如 "activation=['relu','sigmoid']")
* - 错误处理:
* - 如果遇到未知类型(default 分支),直接 LOG(FATAL) 崩溃退出,
* 这是为了在模型导出与运行时解析不一致时能立刻暴露问题,避免 silent error。
* - 扩展性:
* - 如果未来需要支持更复杂的参数类型(如 shape、tensor、dict),
* 可以在 RuntimeParameterType 中新增枚举值,并在此 switch-case 中扩展分支。
*/
void RuntimeGraph::InitGraphParams(
const std::map<std::string, pnnx::Parameter> ¶ms,
const std::shared_ptr<RuntimeOperator> &runtime_operator) {
for (const auto &[name, parameter]: params) {
const int type = parameter.type;
switch (type) {
case int(RuntimeParameterType::kParameterUnknown): {
// 未知参数:只创建一个占位符,不携带任何数据
RuntimeParameter *runtime_parameter = new RuntimeParameter;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterBool): {
// 布尔参数:典型应用如 "bias = true/false"
RuntimeParameterBool *runtime_parameter = new RuntimeParameterBool;
runtime_parameter->value = parameter.b;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterInt): {
// 整型参数:常见于 stride=1, groups=32 等
RuntimeParameterInt *runtime_parameter = new RuntimeParameterInt;
runtime_parameter->value = parameter.i;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterFloat): {
// 单精度浮点参数:常见于 BN 的 eps=1e-5,或 dropout=0.5
RuntimeParameterFloat *runtime_parameter = new RuntimeParameterFloat;
runtime_parameter->value = parameter.f;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterString): {
// 字符串参数:常见于 padding="same" / activation="relu"
RuntimeParameterString *runtime_parameter = new RuntimeParameterString;
runtime_parameter->value = parameter.s;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterIntArray): {
// 整型数组:典型应用如 kernel_size=[3,3],stride=[1,1]
RuntimeParameterIntArray *runtime_parameter =
new RuntimeParameterIntArray;
runtime_parameter->value = parameter.ai;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterFloatArray): {
// 浮点数组:常见于均值/方差数组,如 mean=[0.5,0.5,0.5]
RuntimeParameterFloatArray *runtime_parameter =
new RuntimeParameterFloatArray;
runtime_parameter->value = parameter.af;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
case int(RuntimeParameterType::kParameterStringArray): {
// 字符串数组:如 ["relu", "sigmoid", "tanh"] 这样的配置
RuntimeParameterStringArray *runtime_parameter =
new RuntimeParameterStringArray;
runtime_parameter->value = parameter.as;
runtime_operator->params.insert({name, runtime_parameter});
break;
}
default: {
// 未知类型:立即报错,避免 silent bug
LOG(FATAL) << "Unknown parameter type: " << type;
}
}
}
}
RuntimeParam 设计理念
RuntimeParameter是算子参数的统一抽象基类,用于封装各种超参数。- 通过 基类 + 派生类 的多态结构,可以统一管理 int、float、bool、string 以及数组类型参数。
- 所有参数都存放在
RuntimeOperator::params中,便于解析和使用。 - 每个参数对象带有
type字段用于运行时区分类型。 - 使用虚析构函数保证通过基类指针释放时能正确析构派生类,确保内存安全并支持扩展。
/**
* @brief 运行时算子参数的抽象基类
* @note
* - 作为所有具体参数类型(int/float/string/array 等)的父类使用
* - 统一放置在 RuntimeOperator::params 中,按参数名索引
* - 仅携带最基础的类型信息,其余数据由派生类扩展
*/
struct RuntimeParameter {
virtual ~RuntimeParameter() = default; ///< 保证通过基类指针删除时能正确析构派生类
/// 构造函数,可显式指定参数类型(默认 Unknown)
explicit RuntimeParameter(RuntimeParameterType type = RuntimeParameterType::kParameterUnknown)
: type(type) {}
RuntimeParameterType type = RuntimeParameterType::kParameterUnknown; ///< 参数类型枚举值,用于运行时区分派生类
};